I have seen students hone their skills by borrowing copies of the developer interview books in the Code Fellows “library.” What’s interesting about these books is that they lump questions about graphs and trees into the same chapter.
Technically, trees are graphs. But if you want to show you know what you are talking about during an interview, you need to know when being a graph is important, and when it’s not. (And, maybe, just maybe, you might actually find some of this stuff useful in your career.)
Trees from graphs
Graphs come out of mathematics and are used to describe or model problems. For example, if we wanted to model finding a route for walking from Code Fellows to the foot of the Space Needle, we could represent this using a graph.
A graph is a mathematical structure consisting of a set V of vertices, and a set E of edges, each of which is a pair of vertices.
Our graph of South Lake Union would have a vertex for each place that we have a choice of direction, e.g. outside the Code Fellows door and at each intersection. An edge between two vertices represents the fact that we can walk from one location to the other.
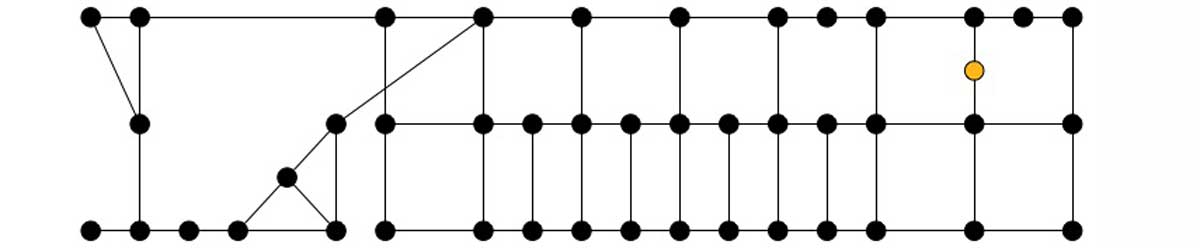
Selecting just part of Seattle to make a graph that covers roads from Code Fellows (yellow) to the Space Needle (blue) gives us 106 vertices and 172 edges.

This graph shows us how we can walk between different locations represented by the vertices.
A chain of vertices connected by edges is called a path, and the way we constructed the graph means that a route on the map is a path in the graph.
The problem of finding a path from one vertex to another is solved using a graph traversal, which is a systematic way of visiting the vertices of a graph.
In our example, we want to find a path from the yellow vertex (Code Fellows) to the blue vertex (the Space Needle), so our traversals will start at the yellow vertex and explore the graph until we reach the the blue one.
The first traversal, called Breadth First Search (BFS), visits all neighbors of each vertex before moving on to another vertex. We do this by holding the vertices to visit in a queue.
BFS(G, s) {
for each vertex v in G {
state[v] = unvisited;
parent[v] = null;
};
state[s] = visited;
queue.enqueue(s);
while (queue not empty) {
u = queue.dequeue();
process(u);
for each vertex v in neighbor(u) {
processEdge(u,v);
if (state[v] == unvisited) {
state[v] == visited;
parent[v] = u;
queue.enqueue(v);
}
}
}
}
The other, called Depth First Search (DFS), follows a chain of vertices until it cannot go further, at which point it backs up. Instead of using a queue, DFS is based on a stack, which means we can just use the call stack with a recursive version:
DFS(G,u) {
state[u] = visited;
process(u);
for each v in neighbors(u) {
processEdge(u,v);
if (state[v] == unvisited) {
parent[v] = u;
DFS(G,v);
}
}
}
Each of these traversals visits the vertices of the graph in a prescribed way
so that we visit the unvisited neighbors of the current vertex.
This gives us a tree (which is captured by the parent array in our pseudo-code).
A tree is a graph that has no cycles (a cycle being a path in the graph that starts and ends at the same vertex).
For instance, in our graph there are a lot of paths that could start and end at the yellow vertex—one represents going out the door, turning left and then taking a left at each intersection until you are back on Boren and at the door again.
Because the traversals ask have I been here? before visiting a vertex, they each construct a tree as they traverse the graph as shown below.

These trees show us the difference between BFS and DFS: BFS methodically visits the three casting a wide net for the search, while DFS runs through the graph following a single path until it either finds what it is looking for or has to backtrack. In this particular problem – searching the graph for any path – DFS can be faster, but it is possible to take the wrong turns and visit the full graph when a shorter path might exist.
For this reason, in Artificial Intelligence, modified versions of these strategies have been developed to solve graph search problems.
These trees are subgraphs of the original graph, and because our problem is really to search for a particular vertex in the graph, they may not actually include all of the vertices in the graph.
However, a tree that does include all of the vertices is called a spanning tree, and these trees are the basis of other kinds of computational problems.
Trees as data structures
We use trees all the time to define data structures as implementations of abstract data types (ADTs) or as the basis for algorithms.
For sets/dictionaries/indexes we have binary search trees, 2-3 trees, B-trees and relatives; for priority queues we have heaps (a form of binary tree); and for pattern matching we have tries and suffix trees.
We are concerned about properties of the tree as a graph, but only because they affect the efficiency of the operations on the tree.
For instance, the length of the paths from the root of a binary search tree to each leaf should be minimized, which happens when the tree is balanced. But, the fact that two binary search trees, where one is balanced and the other is not, are effectively the same, has nothing to do with the properties of the tree as a graph, and everything to do with how the data is organized within the tree.
(Still not with me? Read up on splay trees and ponder how a splay tree’s graphiness is important.)
When we are thinking about trees in data structures, graphs rarely come up. In the mathematical sense, these trees are graphs, but it is helpful to keep the idea of trees as graphs and trees as data structures separate in your head.
Learning more
In the long run, you are going to want to be able to solve problems beyond the interview, and for that I recommend going beyond interview books.
There are a lot of good books andresources for data structures and algorithms—most of which are tailored to a particular programming language.
One of my favorites, which is not tailored this way, is the Algorithm Design Manual by Steven Skiena. The book and website are both good resources on algorithms for graph (and other) problems, and one of the first places I go to remind myself of how to approach a problem.